半径5cm、弧の長さが4πcmである扇形の面積を求めなさい。 これは、中1がこの時期に学習する平面図形の問題の一例です。このように、中心角が出ていない扇形の場合、まずは中止角を求めるのが通常の解き方になります。 中心角をxとおくと、 2×5×π×(x/360)=4π弓形面積 = 扇形面積 - ΔOAB面積(弧の長さ)=(半径)×(円周率)×(中心角)÷180 なので、半径は 半径= 扇形の半径の求め方教えてください! この弧の長さの求め方と 面積の求め方がわからないので

扇形的弧長與面積
弧長 扇形 面積 公式
弧長 扇形 面積 公式- 扇形の半径を求めるときも、面積の公式または弧の長さの公式を利用します。 公式にわかっている値を代入して、「 \(\text{(半径)} = \) 〜 」の形に書き換えていけばいいだけです! 実際に例題を見てみましょう。 例題①「面積がわかっている場合」1431 弧長 同一個定理,按圓形周界同弧長嘅比例 \(弧長 = 2\pi r \times \dfrac{\theta}{360^{\circ}} \) 1432 扇形周界及弓形面積 扇形周界同弓形面積係冇公式的。下面嘅算式只係提大家點計佢地出嚟。 扇形周界 = 弧長 2個半徑;




圓的周長與面積 19 扇形的面積計算 Youtube
Scipursuit 算数・数学 扇形の弧の長さの求め方 公式と計算例 扇形の弧の長さを求める公式は、次の通りです。 l = 2πr× x 360 l = 2 π r × x 360 中心角 x°、半径 r の扇形 ここで、l は扇形の弧の長さ、π は円周率、r は円の半径、x は中心角(単位「度」)を表します。 このページの続きでは、この 公式の導き方 と、 扇形の弧の長さを求める計算問題の解き方 を説明 扇形の面積 = 弧の長さ × 半径 ÷ 2 なんとなく、三角形の面積と同じように面積を求めることができてしまうのです。 では、どうしてこのようなことがいえるかを考えて見ましょう。 扇形の面積を求める公式は前に述べたとおり以下の公式です。 扇形の扇形弧長公式扇形圓周長公式精采文章扇形圓周長公式,橢圓形圓周長公式,正方形周長公式,周長計算公式網路當紅,長方形面積公式,扇形面積公式 1/2(r)^2Θ 弧長公式 r Θ (Θ為角度) 參考資料: 我自已 1 001 意見者: MrNatural ( 初學者 2 級 ) 發表時間: 0145 檢舉 ~老人家 ,弧長公式n是
おうぎ形の公式 弧の長さ = 円周 × 中心角 360° 中 心 角 360 ° = 直径×314 × 中心角 360° 中 心 角 360 ° おうぎ形の面積 = 円の面積 × 中心角 360° 中 心 角 360 ° = 半径×半径×314 × 中心角 360° 中 心 角 360 ° 重要なのは、 おうぎ形が元の円と比べた時にもしくは、単純に、1ラジアンの円弧の長さ(=半径(r))の θ倍であるため ・扇形の面積は (r 2 θ)/2 扇形の面積の公式:円弧×半径/2 に代入 もしくは、円全体の面積 πr 2 に割合 θ/2π を掛ければ數學 扇形面積公式,大家都在找解答 第1頁。圓的面積計算方式。 8s21 能理解弧長的公式以及扇形面積的公式。 圓弧長度= × 2 半徑π × 360 q × , q為圓弧所對的圓心角度數。 扇形面積= 半徑×半徑 ,圓的扇形,面積是多少平方公分?
C 扇形弧長S=rθ d 扇形面積A=1 2 r2θ=1 2 rS (2)三角函數的定義 正弦函數sinA=∠ 的對邊 斜邊 餘弦函數cosA=∠ 的鄰邊 斜邊 正切函數tanA=∠ 的對邊 ∠ 的鄰邊 餘切函數cotA=∠ 的鄰邊 ∠ 的對邊 正割函數secA= 斜邊 ∠ 的鄰邊 餘割函數cscA= 斜邊 ∠ 的對邊 (3)三角函數的關係扇形的弧長與面積 扇形的弧長與面積 1弧長扇形的弧長我們要怎麼求得呢 2扇形面積 這樣以後題目給我們半徑r,跟角度要我們求扇形的弧長或面積,我們就可以輕鬆的套公式把它算出來了 弧の長さ,面積がシンプル: 上記の「弧の長さと面積の公式」を見ると度数法よりも弧度法の方がややシンプルです。 これは弧度法の利点です。 しかし,この程度では「度数法よりも弧度法の方が優れている」という強い理由にはならないと思います。



扇形面积计算公式 万图壁纸网




扇形周长公式和面积公式是什么 星火网校
「扇形の面積の公式」を忘れたら「ピザ」を思い出そう笑 まとめ:扇形の面積は「おうぎ形パワー」を円にかける 扇形の面積の求め方はどうだった?? 円の公式に毛がはえたようなもんだから、頑張れば覚えられそうだね。 S = πr² × α / 360扇形的弧長與面積公式: 若圓半徑為 r ,扇形 COD 的圓心角 ∠ COD =θ(弧度),0 ≤ θ ≤ 2π, 如下圖所示,令扇形的弧長為 s ,面積為 A ,則:扇形の面積を求める公式は、次の通りです。 S = πr2 × x 360 = 1 2lr S = π r 2 × x 360 = 1 2 l r 中心角 x°、半径 r の扇形 ここで、S は扇形の面積、π は円周率、r は円の半径、x は中心角(単位「度」)を表します。 また、2行目の l は扇形の弧の長さを表します。 このページの続きでは、この 公式の導き方 と、 扇形の面積を求める計算問題の解き方 を説明しています



Q Tbn And9gctoaftep Cp0mxb1byahotggx3ub73wafwbkzah7fg7xmsh2anr Usqp Cau



圆的周长与面积 弧长 扇形的面积 玄数
數學領域數學 學習階段: 國小56年級 (三) 學習內容: S63 圓周率、圓周長、圓面積、扇形面積:用分割說明圓面積公式。 求扇形弧長與面積。 知道以下三個比相等:(1)圓心角:360;(2)扇形弧長:圓周長;(3)扇形面積:圓面積,但應用問題只處理用(1)求弧長或面積。 學習表現: sⅢ2 認識圓周率的意義,理解圓面積、圓周長、扇形面積與弧長之計算方式。θ ( 2) e l l i p t i c a l a r c h L = a E ( x ( θ 0) a, k) − a E ( x ( θ 1) a, k) x ( θ) = r ( θ) cos θ, k = 1 − ( b a) 2, a ≥ b, π 2 ≥ θ ≥ 0 E ( x, k) 2 n d i n c o m p l e t e e l l i p t i c i n t e g r a l 関連リンク 楕円の弧長の求め方 お客様の声 アンケート投稿 よくある質問 円・扇形の公式まとめ 円周: 2πr 2 π r 円の面積: πr2 π r 2 扇形の弧の長さ: 2πr× a 360 2 π r × a 360 扇形の面積: πr2 × a 360 π r 2 × a 360 扇形の面積(弧の長さ l l からの導出): 1 2lr 1 2 l r ※半径: r r 、円周率: π π 、中心角: a a 、扇形の弧の長さ: l l それぞれについて詳しく見ていきましょう。



第二十四章圆24 4 弧长和扇形面积第1课时弧长和扇形面积学练优九年级数学上 Rj 教学课件优翼课件导入新课讲授新课



扇形面积计算圆扇形弧形计算公式谁有计算圆弧长扇形面积和圆锥的面积的公式 尚书坊
おうぎ形の半径と中心角を入力して「計算」ボタンを押すと、おうぎ形の面積と弧の長さが計算されます。 円周率は変更できます。 円周率で「πを使う」にチェックを入れると円周率をπとして計算します。 半径を求めたい場合は、中心角と面積もしくは弧の長さと面積の公式 <証明> 弧の長さと面積の公式の証明をしておきます。 証明が必要ない方は、次の章へ進んでください。 扇形の弧の長さ 扇形の弧の長さは中心角の大きさに比例する。 中心角が2倍になれば、弧の長さも2倍になる。 扇形のまわりの長さは、 扇形の弧の長さ+半径×2 で求められます。 この扇形の弧の長さ=18×314× 1 ° 360 ° =14(cm) よって、求める扇形のまわりの長さは 14+9×2=3684(cm) 答え 3684㎝ ~平面図形の面積・まわりの長さを求める公式まとめ



Q Tbn And9gcr6gw9fhpzovmfob2ngp9u Gvimmrq94zqc64t Ysfbxqs9wsbi Usqp Cau



扇形面积练习题 弧长公式 扇形面积式及其应用 含经典习题 尚书坊
扇形面积公式描述了扇形面积和圆心角(顶角)、半径、所对弧长的关系。 数学公式表示为:S扇=(lR)/2 (l为扇形弧长) =(1/2)θR²(θ为以弧度表示的圆心角)。直交座標系表示の時の弧長 \(xy\) 直交座標系で曲線が \(y = f(x)\) で表される時、この曲線の区間 \(a, b\) の弧長 1弧長扇形的弧長我們要怎麼求得呢 2扇形面積 這樣以後題目給我們半徑r,跟角度要我們求扇形的弧長或面積,我們就可以輕鬆的套公式把它算 扇形の公式はこう変わる 弧度法の定義は扇形の弧の長さ を半径 で割ると, 角 が求まるというもので, 以下の式で定義されます。 この定義から, 扇形の弧の長さ は, と導け, 扇形の面積 は, 度数法の公式 をradに置き換えて, また, 扇形の弧の長さの公式より



扇形面积计算圆扇形弧形计算公式谁有计算圆弧长扇形面积和圆锥的面积的公式 尚书坊




1x秋九年级数学上册第二十四章圆24 4弧长及扇形的面积第1课时弧长和扇形面积教案2 新版 新人教版下载 Word模板 爱问共享资料
扇形的弧長與面積 1弧長扇形的弧長我們要怎麼求得呢 2扇形面積 這樣以後題目給我們半徑r, 則 s(t) 可以想像為動點從時間 a 出發,b分別為長軸半長與短軸半長 假定我們想計算等角螺線 上,2, 一個估計 之弧長的方法, 則About Press Copyright Contact us Creators Advertise Developers Terms Privacy Policy & Safety How works Test new features Press Copyright Contact us Creators求扇形弧長與面積。知道以下三個比相等:(1)圓心角:360;(2)扇形弧長:圓周長;(3)扇形面積:圓面積,但應用問題只處理用(1)求弧長或面積。 學習表現: sⅢ2 認識圓周率的意義,理解圓面積、圓周長、扇形面積與弧長之計算方式。 議 題:



扇形弧长怎么算 西瓜视频搜索



高一 高一期末复习专题 6 弧长公式 扇形面积公式
面積和體積 >> 這是一個初中學生年年都要學嘅課題。喺中一嘅時候大家其實只經學咗不少,中二加嘅面積公式主要係扇形嘅面積同弧長。其實只要明白公式入面嘅符號 r, h等代表咩,計數時大部份都係代數字、解方式。唔會太難, 只係題目會一年比一年深(但唔代表難咗)。為求得此弧邊面積,先以正五邊形作為試驗 ── 分割中央弧邊面積 先將中央弧邊面積以OB OC中心分割成五分之一,並連──接 AB AC 。且 OBC面積 = 扇形ABC面積 – 2 ΔOAB面積。 ── おうぎ形の公式おうぎ形の面積は、半径をr、面積をS、円周率をπ、中心角をαとすると、S = πr² × α / 360となります。つまり、円周率×半径×半径×中心角÷360です。たとえば、半径3cm、中心角が90度の扇形があったとします。扇形の公式にあてはめるとS = 3×3×π×90/360= 9π/4となります。扇形の



Ch2三角函數 2 1 2 2 我的m讚



Search Q E6 87 E5 E5 85 Ac E5 8f Tbm Isch
馬雲:看懂了,等於讀了 3 年 mba! 你不成熟的4大特徵 "扇形の弧の長さと面積"の公式とその証明です! 扇形の弧の長さと面積公式扇形の弧の長さと面積半径r、中心角θ、弧の長さl、面積Sとすると \(・l=rθ\) \(・S=\frac{1}{2}r^2θ=\frac{1}{2}lr\)証明式 扇形 A = 面積 L = 円周の長さ R = 半径 扇形 A = 面積 L = 弧の長さ α = 角度 (DEG) α = 角度 (rad) A = 面積 L = 弧の長さ α = 角度 (DEG) α = 角度 (rad) 弓形



扇形面积的计算公式 扇形面积的计算公式画法




扇形弧長 扇形弧長是扇形的兩條半徑之間的圓弧長度 一條圓弧和經過這條圓弧 百科知識中文網
2分でわかる!扇形の弧の長さを求める公式 「扇形の弧の長さ」の求め方の基本はわかったね?? それじゃあ、 扇形の弧の長さの公式 をみていこう! 扇形の半径をr、中心角をα、円周率をπとすると、 2πr×α/360 で「扇形の弧の長さ」を求められるんだ。扇形の面積・弧の長さ・まわりの長さの求め方公式 =直径×円周率× 中 心 角 360 ° +半径×2 ピタグラスの定理(三平方の定理)により,横の長さが Δx,縦の長さが Δy である直角三角形の斜辺の長さ ΔL は したがって x ,y 直交座標では x=t とおけば上記の公式が得られる.



弧长和扇形面积 圆ppt下载 第一ppt




Ppt 弧长和扇形面积powerpoint Presentation Free Download Id




圓中有關計算 弧長 扇形面積和圓錐




扇形面积公式 弧长和扇形面积 52fmz购物网



功課幫




扇形計算公式 一條弧和經過這條弧兩端的兩條半徑所圍成的圖形叫扇形 半 華人百科




扇形的弧長與面積




初三數學 扇形的面積 空間想像不好的同學 請記住這些知識點 每日頭條




圆中有关计算 弧长 扇形面积和圆锥




扇形面积怎么算怎样求扇形的面积



扇形面积计算器 弧长及扇形的面积计算公式 尚书坊




九年級數學 圓 弧長和扇形面積 每日頭條




09 11 27 01 圓與扇形 不學無數 隨意窩xuite日誌
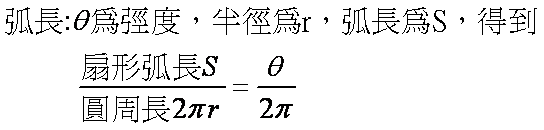



扇形的弧長與面積




24 4弧长和扇形面积圆锥的侧面积和全面积 Ppt Download




09 11 27 01 圓與扇形 不學無數 隨意窩xuite日誌



扇形面积计算圆扇形弧形计算公式谁有计算圆弧长扇形面积和圆锥的面积的公式 尚书坊



最新 24 4弧长和扇形面积 第1课时 课件 Ppt 课件巴巴kejian Com 课件巴巴kejian Com



扇形面积公式 弧长公式与扇形面积公式 尚书坊



弧长和扇形面积 圆ppt课件2下载 课件之家




2 圓心角所對弦長 弧長與扇形面積 基本觀念 國三上2 2 Live數學學習網 Www Liveism Com 名師葛倫 Youtube



弧长和扇形面积 圆ppt 第一课时 第一ppt



圆弧面积计算公式图解 图片欣赏中心 急不急图文 Jpjww Com




弓形 圆弧形的面积 弧长 弦长 弦高 半径 夹角在线计算器 三贝计算网 23bei Com



扇形的弧长怎么计算 西瓜视频搜索



圆弧面积计算公式图解 图片欣赏中心 急不急图文 Jpjww Com



扇形弧长公式 扇形弧长公式画法



三角公式怎么记 请看这儿




扇形的面积 弧长 周长 弦长在线计算器 三贝计算网 23bei Com



扇形面积计算公式图解 万图壁纸网




人教版九年级数学上24 4 1弧长和扇形面积同步练习卷含答案 Doc 文档分享网



扇形的面积 教案 教师资格面试初中数学 试讲技巧 安徽民师教师招聘考试网




例題 如何計算扇形的弧長 數學 均一教育平台




弧長計算公式 弧長公式 N是圓心角度數 R是半徑 L是圓心角弧長 L 華人百科




扇形面积计算公式如何推导 教育频道 手机搜狐



弧长和扇形面积 圆ppt 第1课时 第一ppt




Ppt 弧长和扇形面积powerpoint Presentation Free Download Id



扇形的面积公式 哔哩哔哩 つロ干杯 Bilibili




圓的周長與面積 19 扇形的面積計算 Youtube




扇形弧長及面積 每日頭條



九年级数学上册24 4弧长及扇形的面积24 4 1弧长和扇形面积 学案 新人教版 Doc 课件巴巴kejian Com 课件巴巴kejian Com




圆中有关计算 弧长 扇形面积和圆锥



3 9 弧长及扇形的面积 哔哩哔哩 つロ干杯 Bilibili




扇形面积怎么算怎样求扇形的面积




扇形的面积公式 弧长公式 环球信息网




圓的周長與面積 27 扇形的複合圖行計算2 Youtube



1 一个半径为r的扇形 若它的周长等于弧所在的半圆的长 那么扇形的圆心角是多少弧度 是多少度 扇形的面积是多少 2 一扇形的周长为 高中 数学试题 弧度制 弧度与角度的互化考点 任意角的三角函数考点 好技网



扇形面积的计算公式 扇形面积的计算公式画法



圓心角所對弦長 弧長與扇形面積 Live 多媒體數學觀念典online




高中數學 三角函數 數乙 弧長與扇形面積公式i 曾政清 Youtube
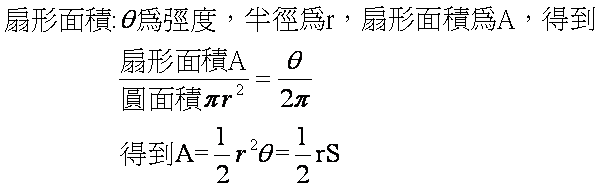



扇形的弧長與面積




圓中有關計算 弧長 扇形面積和圓錐




高中數學 三角函數 數乙 弧長與扇形面積公式ii 曾政清 Youtube




九年級數學 圓 弧長和扇形面積 每日頭條



扇形面积的计算公式 扇形面积的计算公式画法



扇形面积计算圆扇形弧形计算公式谁有计算圆弧长扇形面积和圆锥的面积的公式 尚书坊




扇形的周长和面积公式是什么



高中数学扇形弧长公式 西瓜视频搜索



九年级数学上册24 3圆与多边形4弧长扇形面积圆锥表面积计算课件 新人教版 莲山课件



圆弧面积计算公式图解 图片欣赏中心 急不急图文 Jpjww Com



扇形面积公式讲解 北京爱智康



圆弧面积计算公式图解 图片欣赏中心 急不急图文 Jpjww Com




扇形周長與面積 6年級數學 Grade 6 Math Fan Shaped Area Youtube
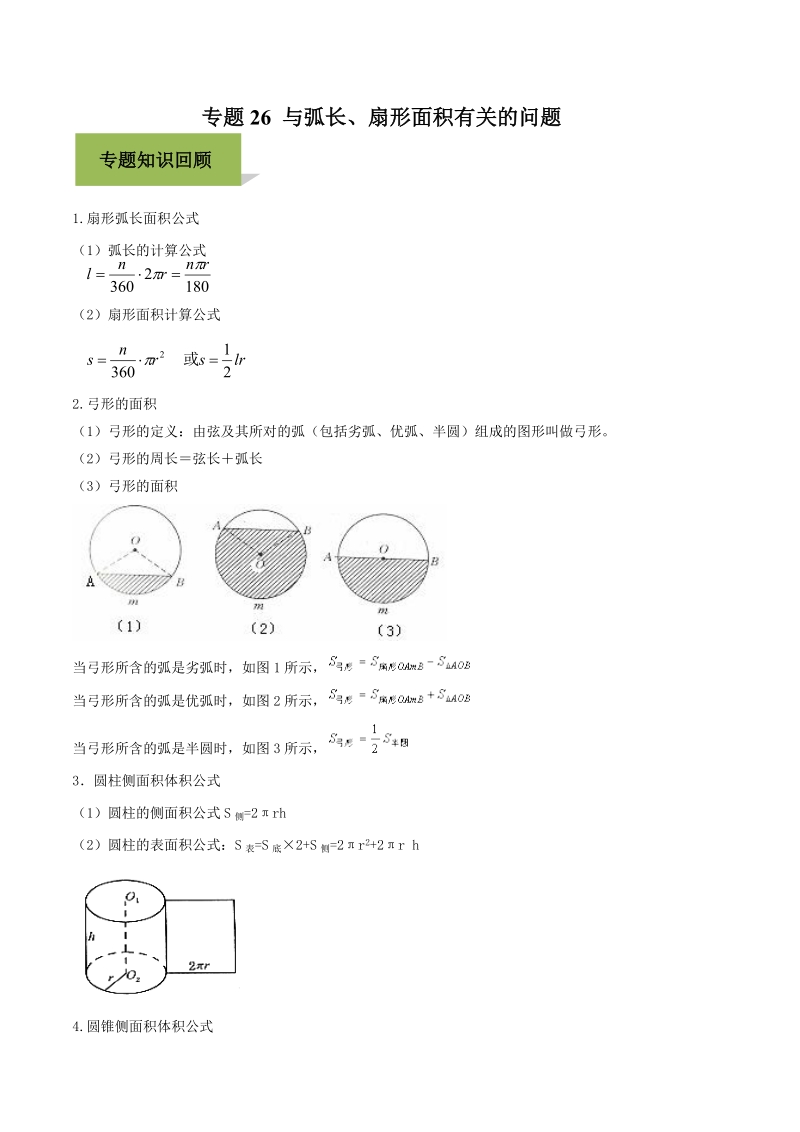



年中考数学必考专题26与弧长 扇形面积有关的问题 原创版 七七文库www 77wenku Com



5 4 扇形周長和面積 高市資教中心教材網




数 你好看 任意角三角函数与诱导公式 知乎



六年级扇形面积和弧长公式 中国教育网
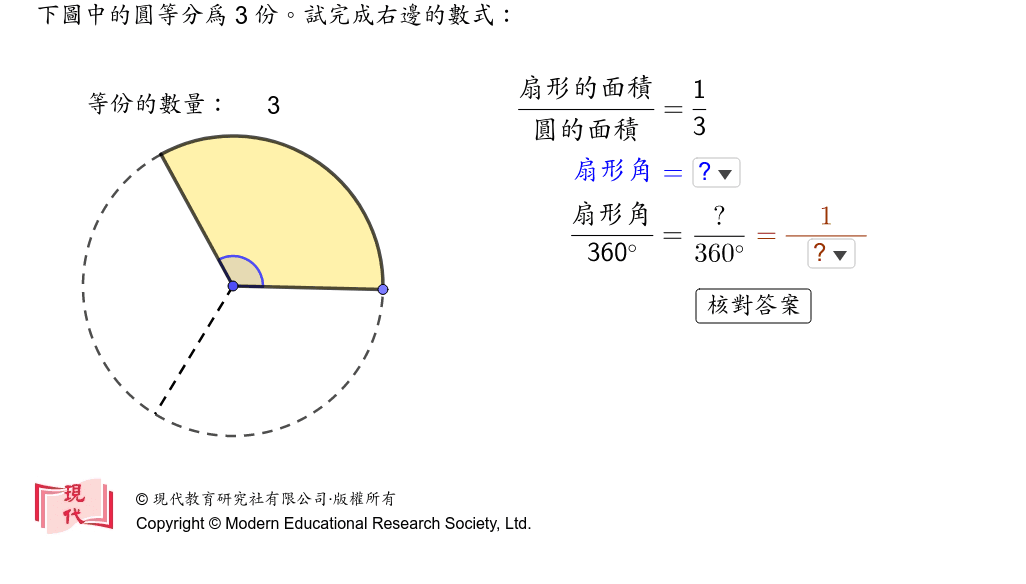



扇形面積公式 Geogebra




09 11 27 01 圓與扇形 不學無數 隨意窩xuite日誌




360影视 影视搜索



扇形面积计算圆扇形弧形计算公式谁有计算圆弧长扇形面积和圆锥的面积的公式 尚书坊




圓的周長與面積 16 扇形弧長計算的練習 Youtube




扇形面積公式 公式 推導過程 注意事項 中文百科全書



弧度制扇形面积公式高中扇形的弧长和面积公式 图文 叽叽歪歪吧




扇形面積公式弧長14 Zilhc




扇形面積公式弧長14 Zilhc




圆中有关计算 弧长 扇形面积和圆锥



弧长公式 扇形面积公式 圆 中考网




扇形弧長及面積 每日頭條




001 弧度 弧長及扇形面積原理 Youtube




高中數學必修四 三角函數突破點 二 弧度制及其應用 每日頭條




扇形面积公式和扇形弧长公式扇形的所有公式



Q Tbn And9gcqpqxxknzceay3mjcxzcklaz Iozcfat84mkqdgzflcwlamy23 Usqp Cau



证明扇形面积与弧长公式圆锥的侧面积为什么会等于prl 扇形面积公式推导兀rl 桃丽网



扇形面积和弧长公式 搜狗图片搜索



扇形面积的计算公式的应用 28 5弧长和扇形面积的计算 初中冀教版13版 数学中国网 Mathschina Com
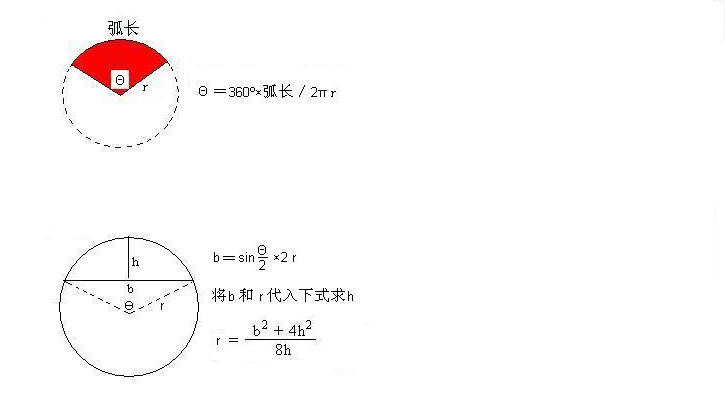



弧長計算公式 計算公式 弧長公式 拓展 例子 補充公式 各種公式 扇形面積 公式 中文百科全書




16年中考數學試題彙編 弧長與扇形面積 每日頭條



0 件のコメント:
コメントを投稿